Housing, Land and Property Taxes - Advanced
UCLA - Econ 221 - Advanced Macro
François Geerolf
November 26, 2019
Some resources
Bibliography
- ECB: https://www.ecb.europa.eu/pub/pdf/other/mb201008_focus06.en.pdf
- Eurostat Manual:
BEA U.S.
Underlying GDP by Industry
OECD / Eurostat Data / IMF : ILO
PRICES_CPI

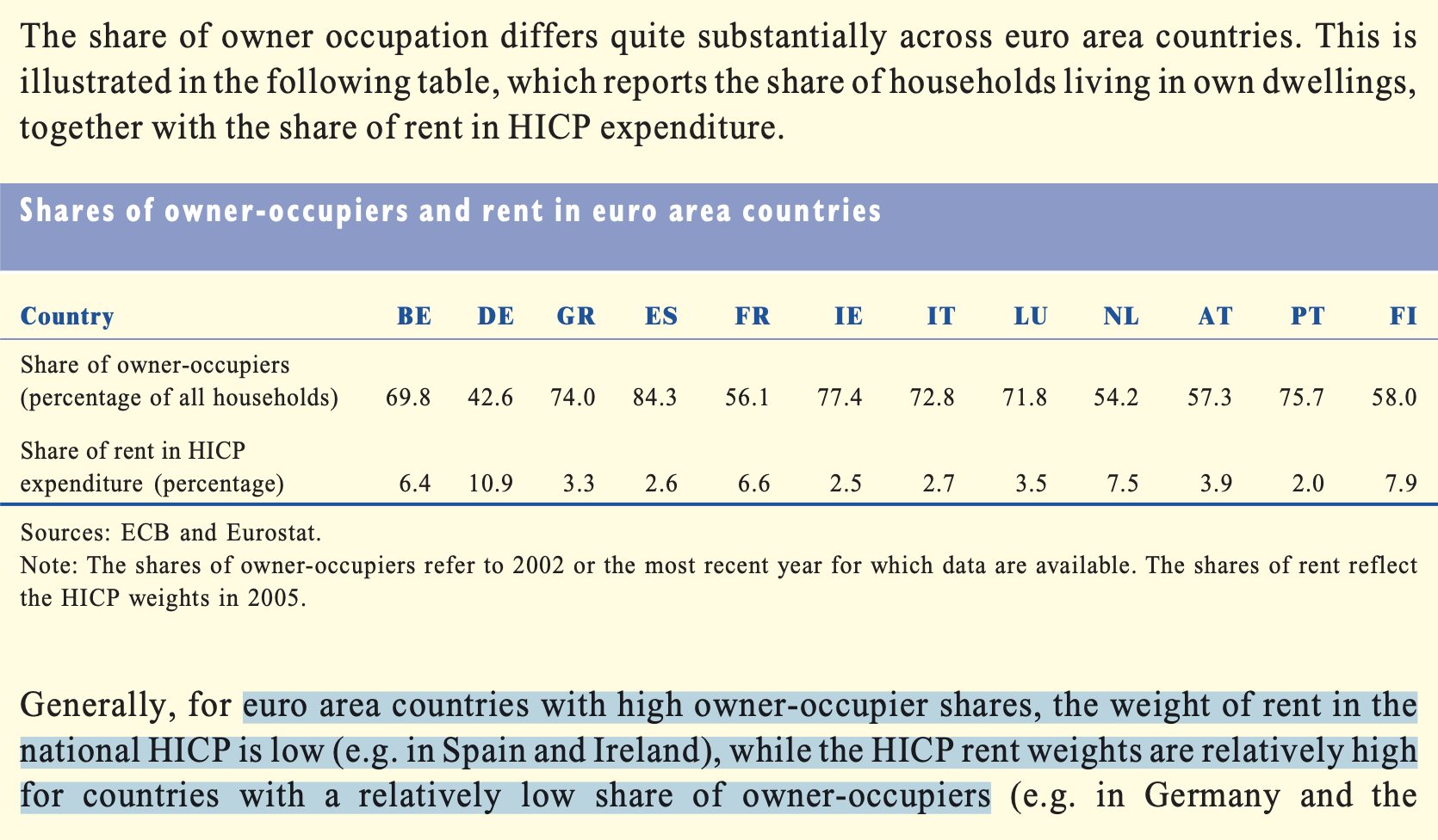
Housing in the Price Index

Housing in the Price Index
English
French
Eurostat
Eurostat

Eurostat
Eurostat

ILO

ILO
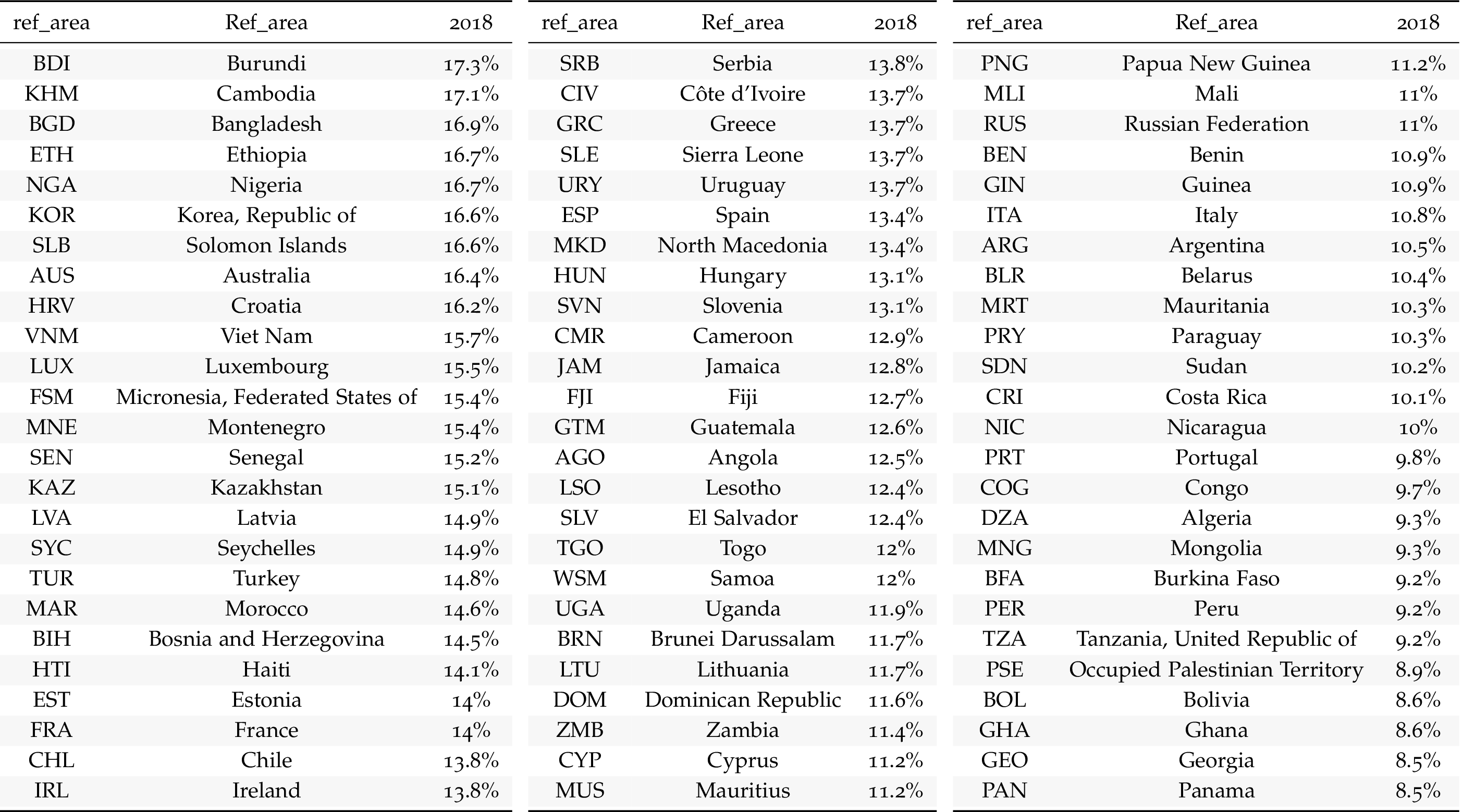
IMF - CPI - (Monthly only)

IMF - CPI - (Quarterly only)
Problem: the way it’s accounted for

France, Austria and Spain

Germany - Destatis
2-digit
3-digit

Dallas Fed Data
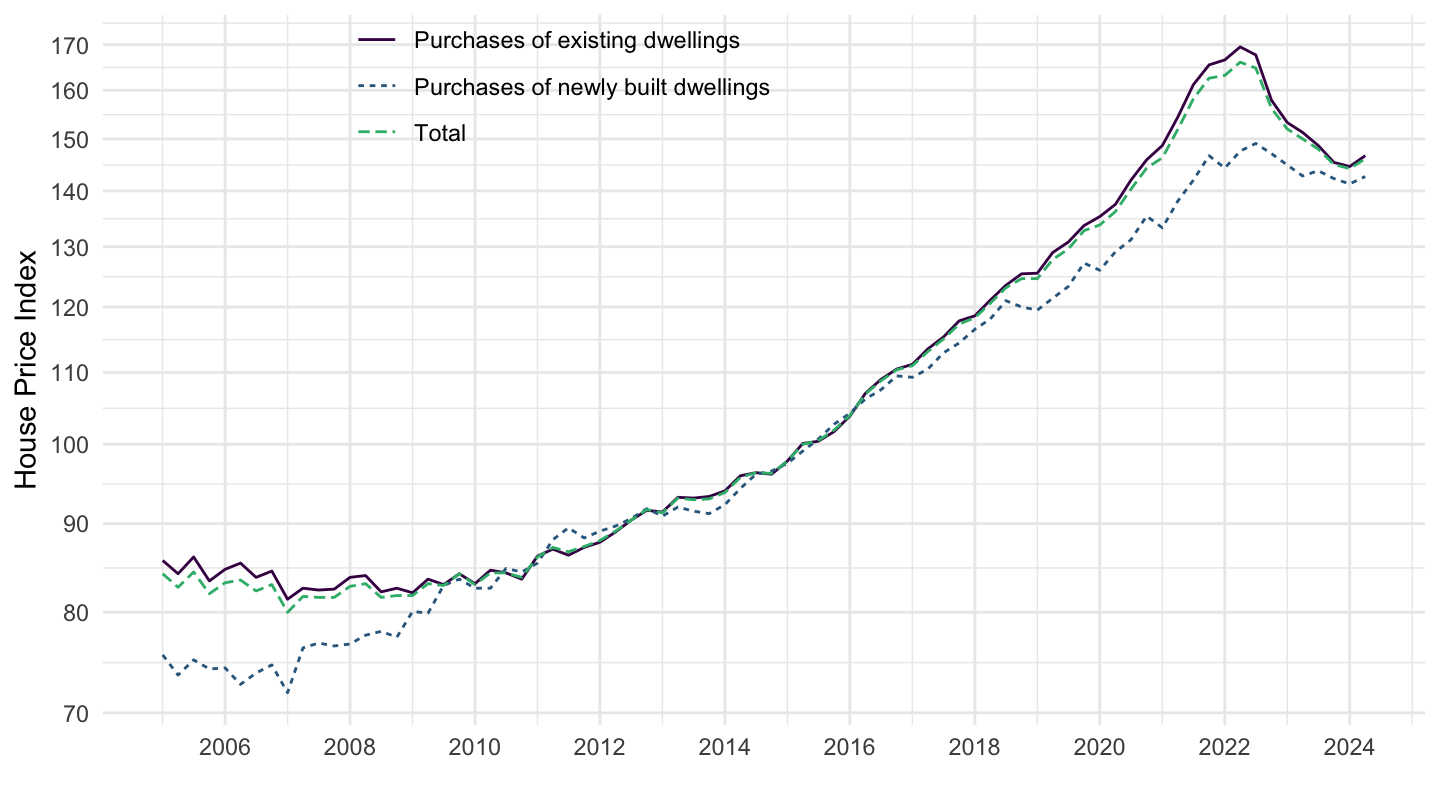
Real House Prices
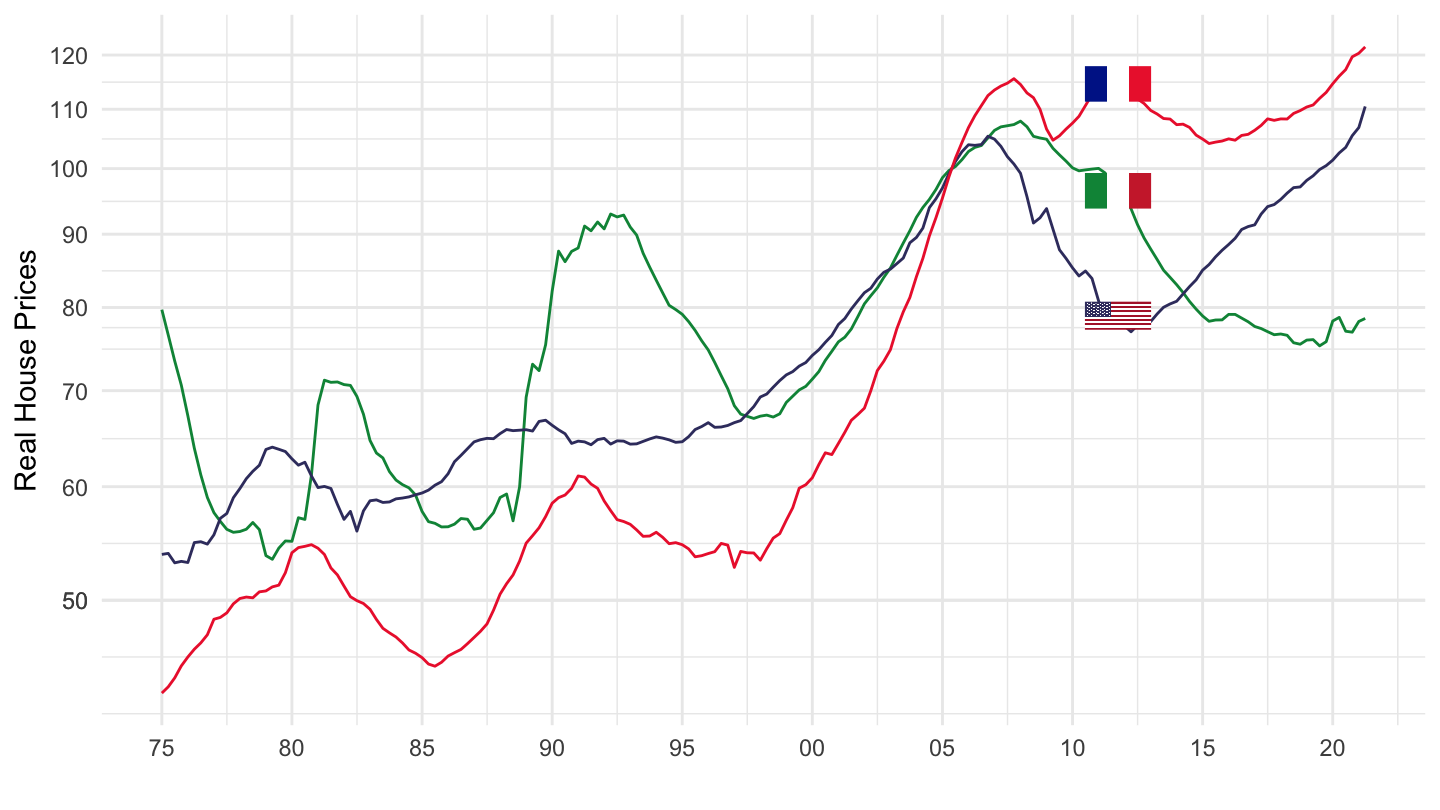
House Prices
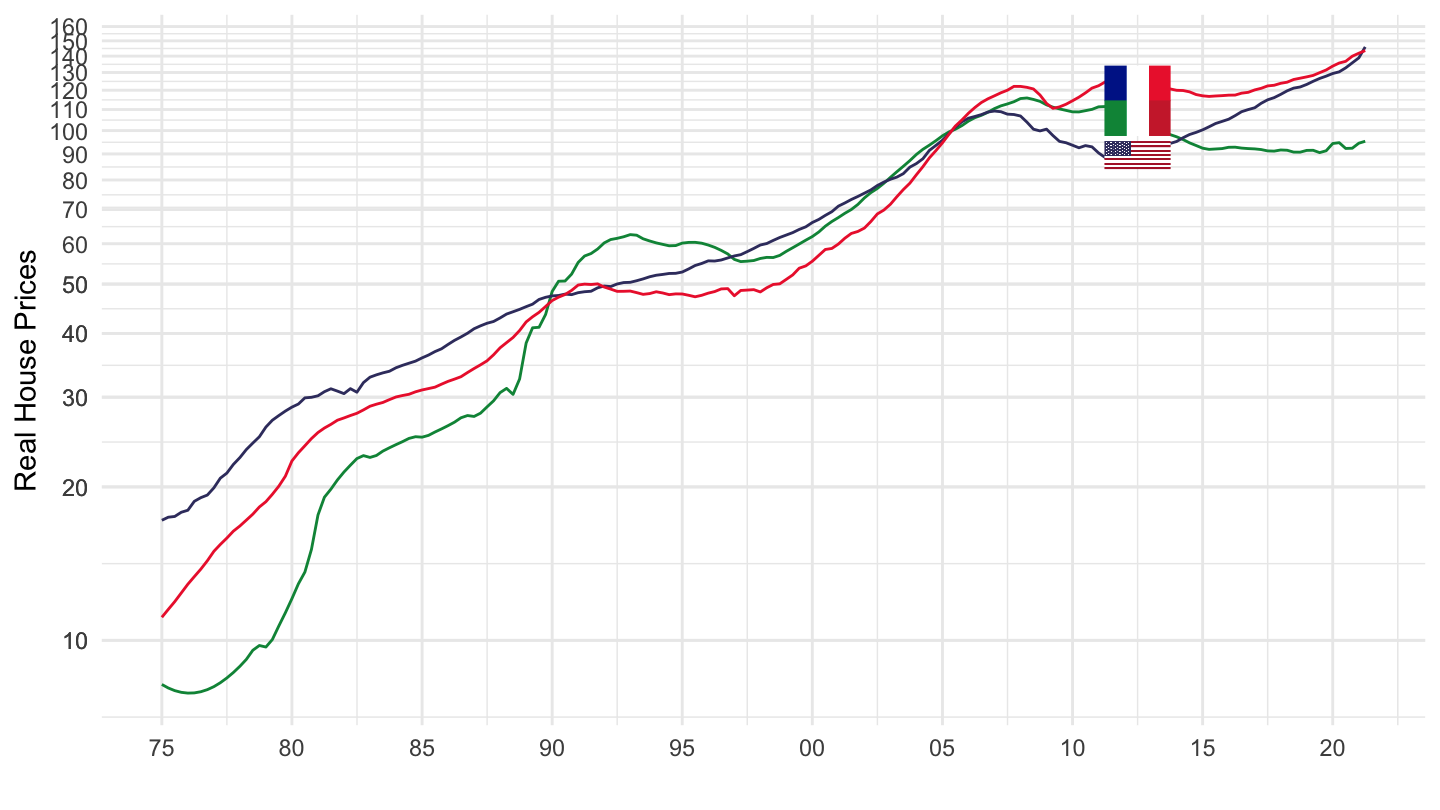
Eurostat Data
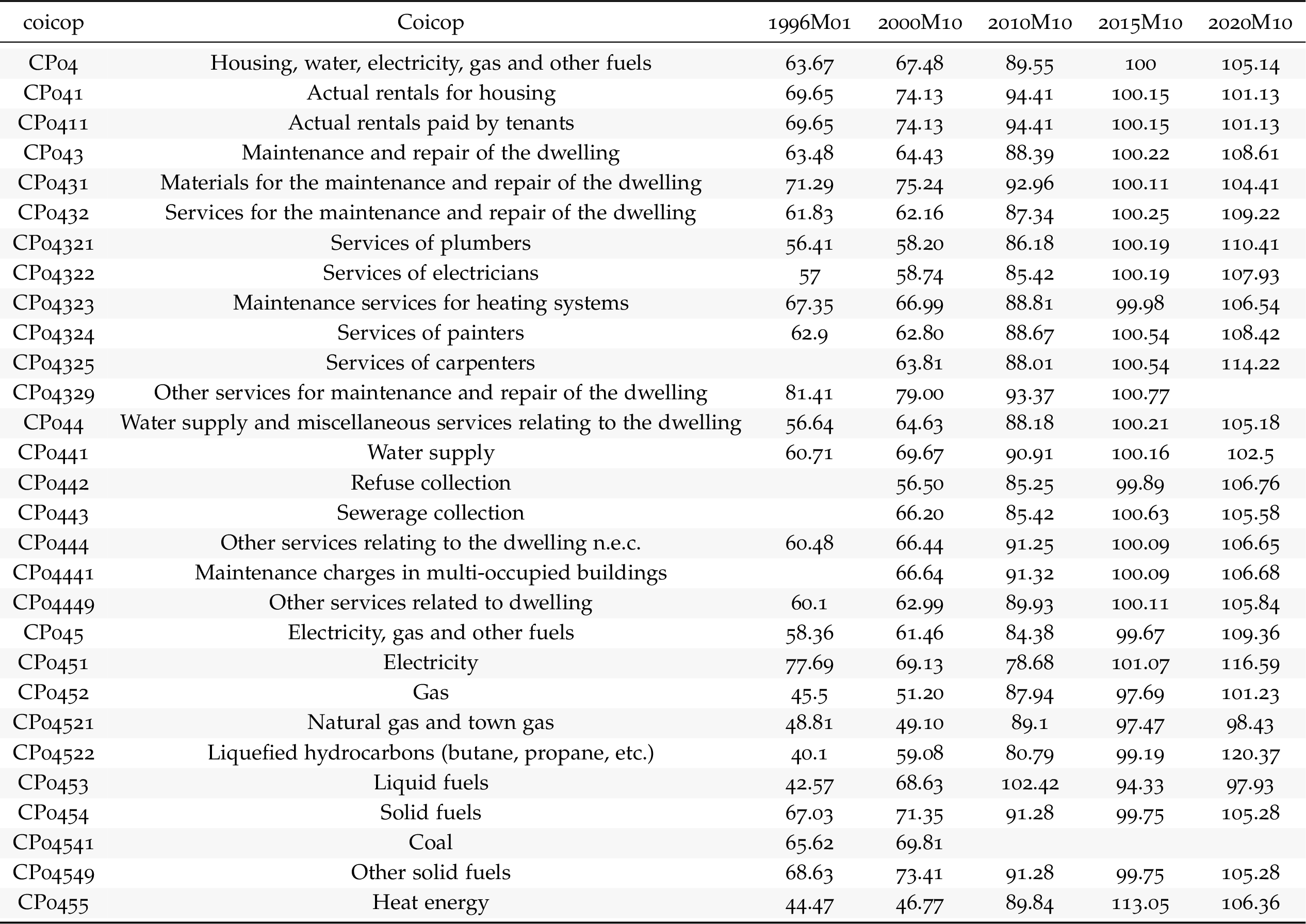
Sub-index weights

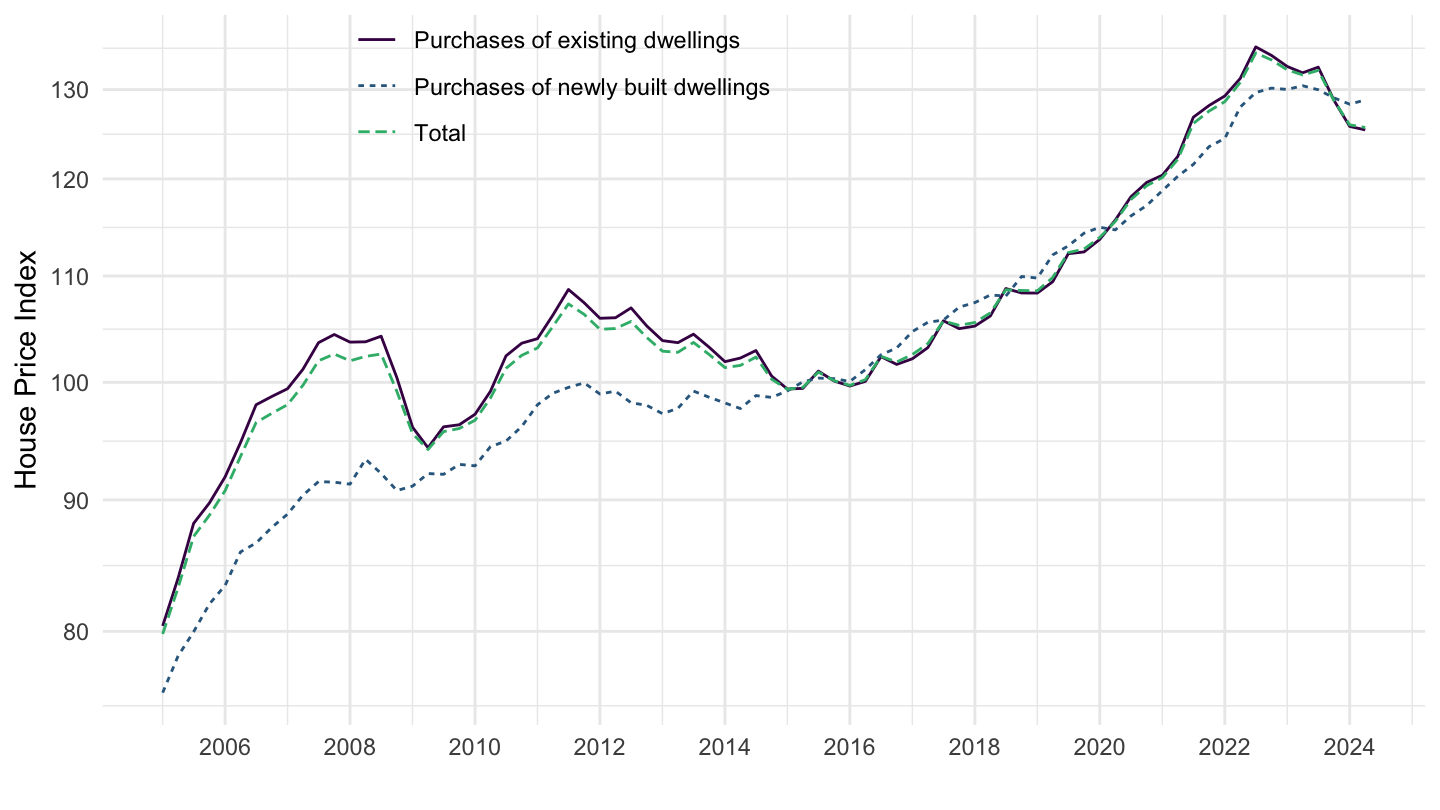
Existing VS New Dwellings Price Index

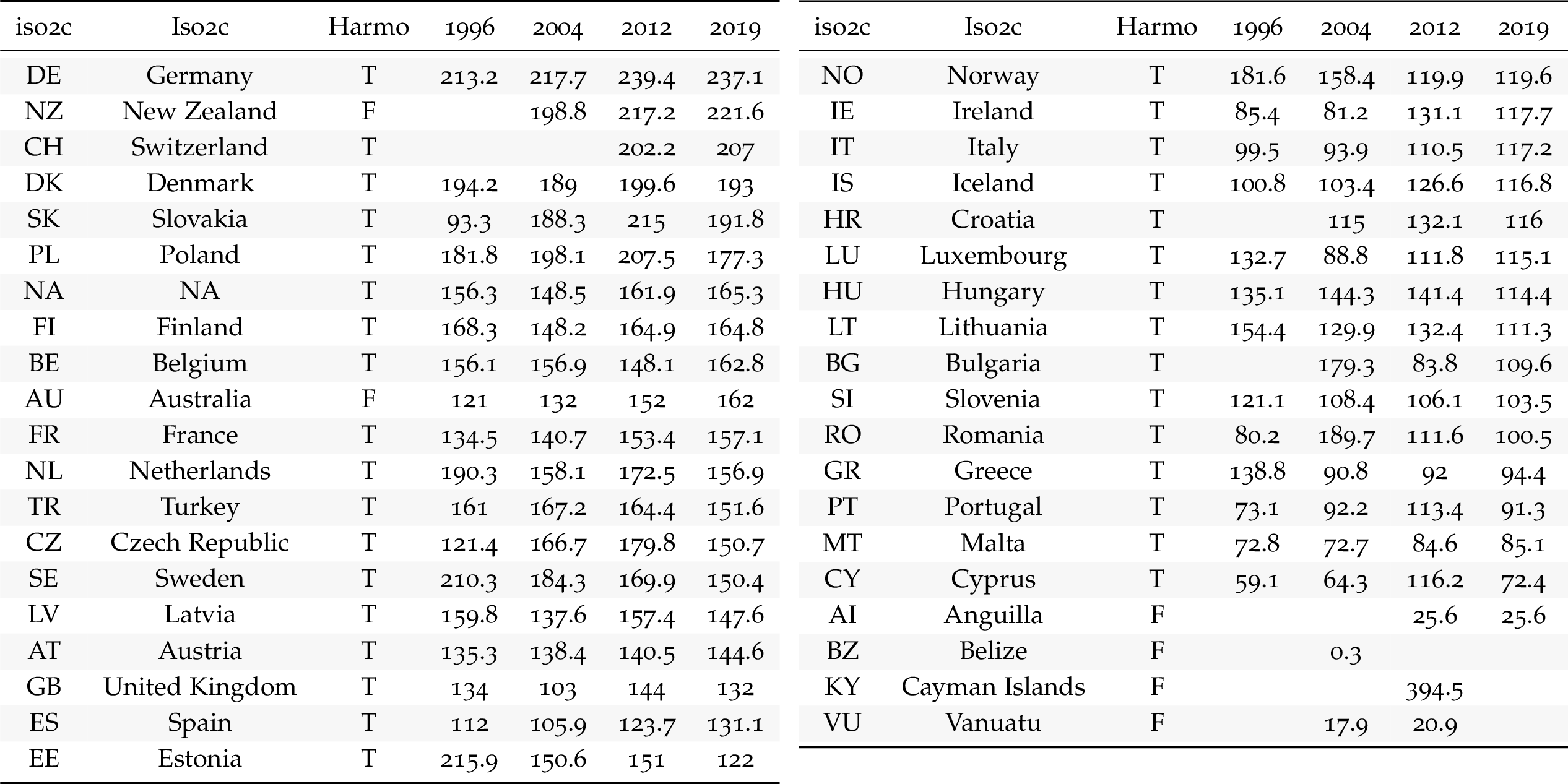
Harmonized owner-occupied housing

Harmonized owner-occupied housing

France
Actual / Imputed Rentals - France
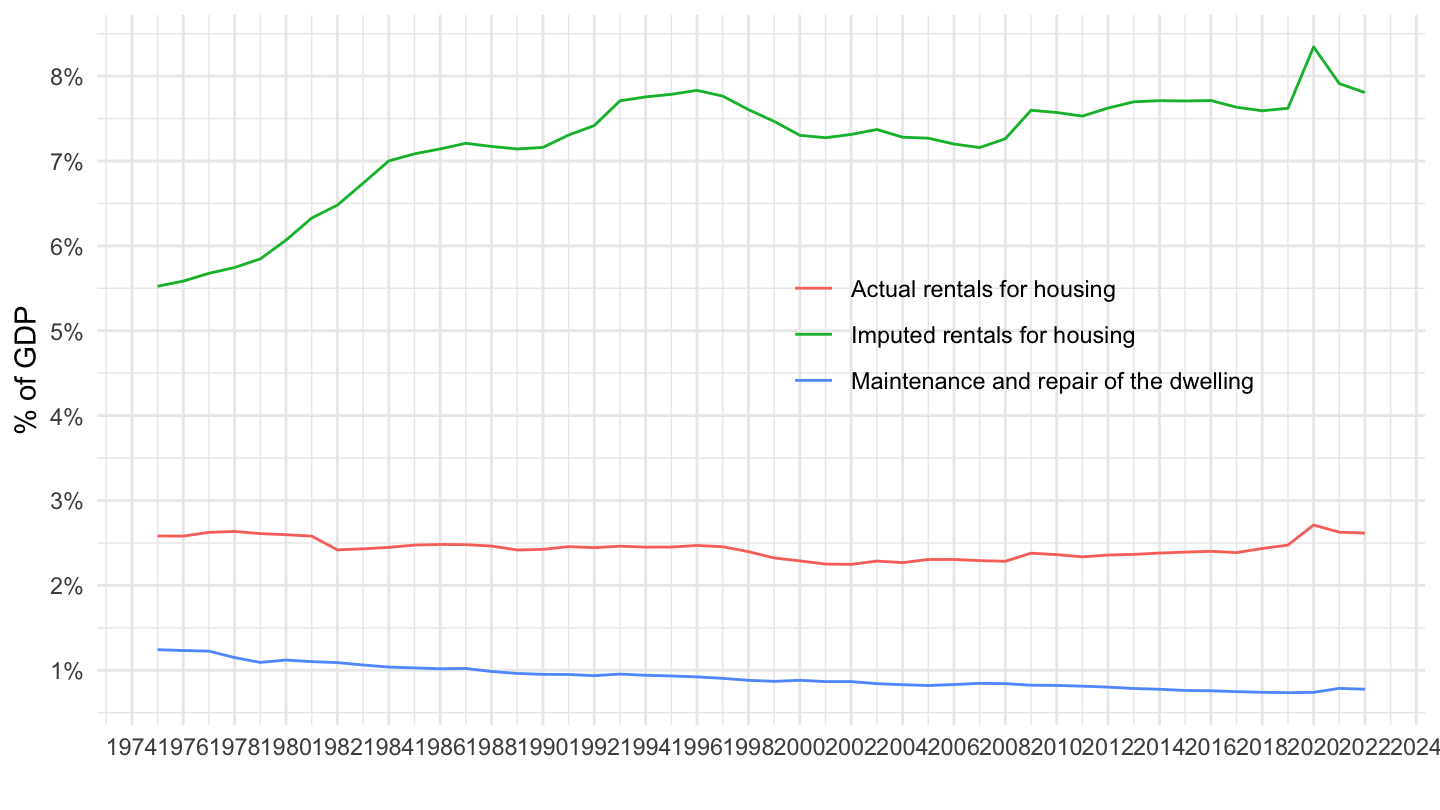
Actual / Imputed Rentals - France

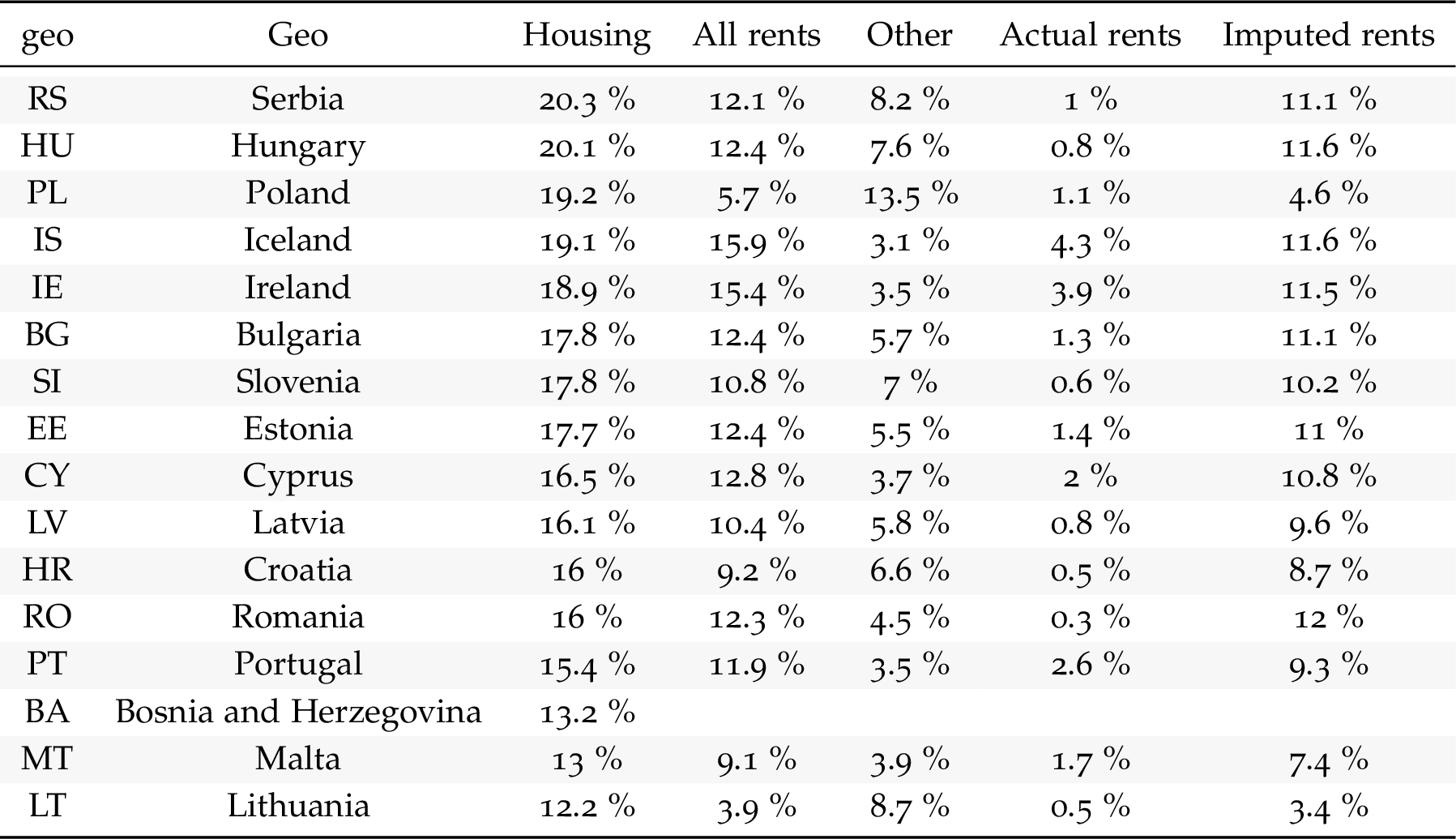
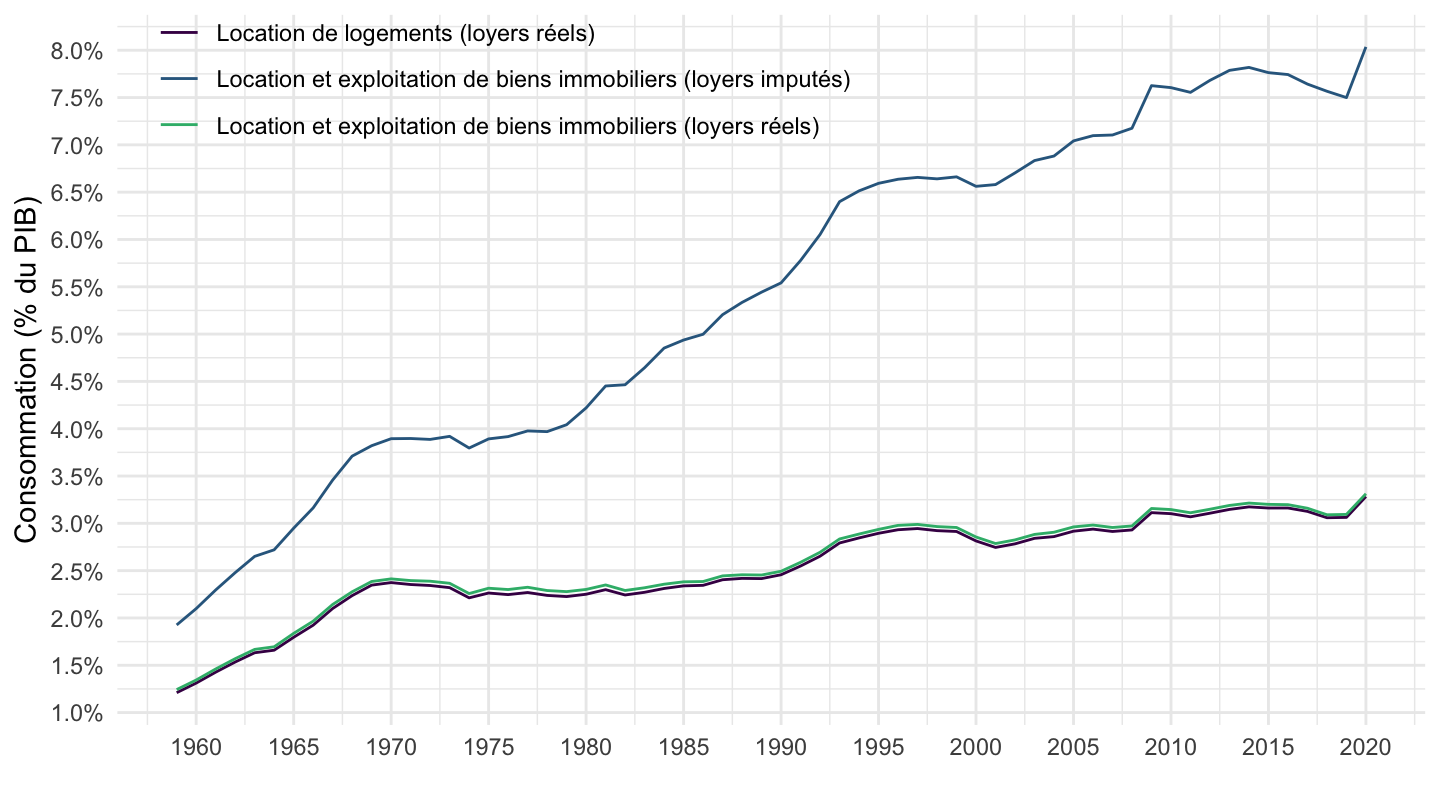
Consumption: Imputed VS Actual Rentals

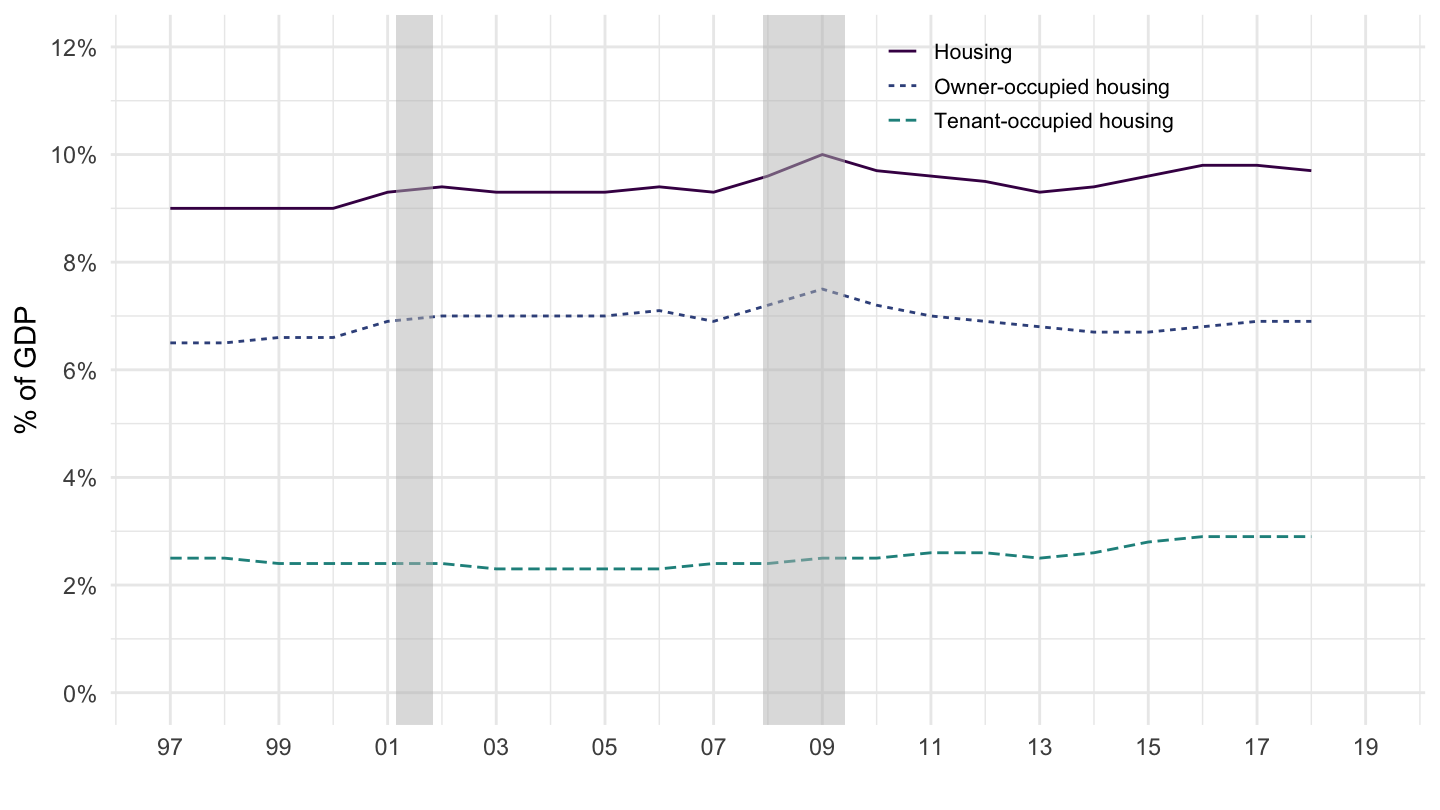
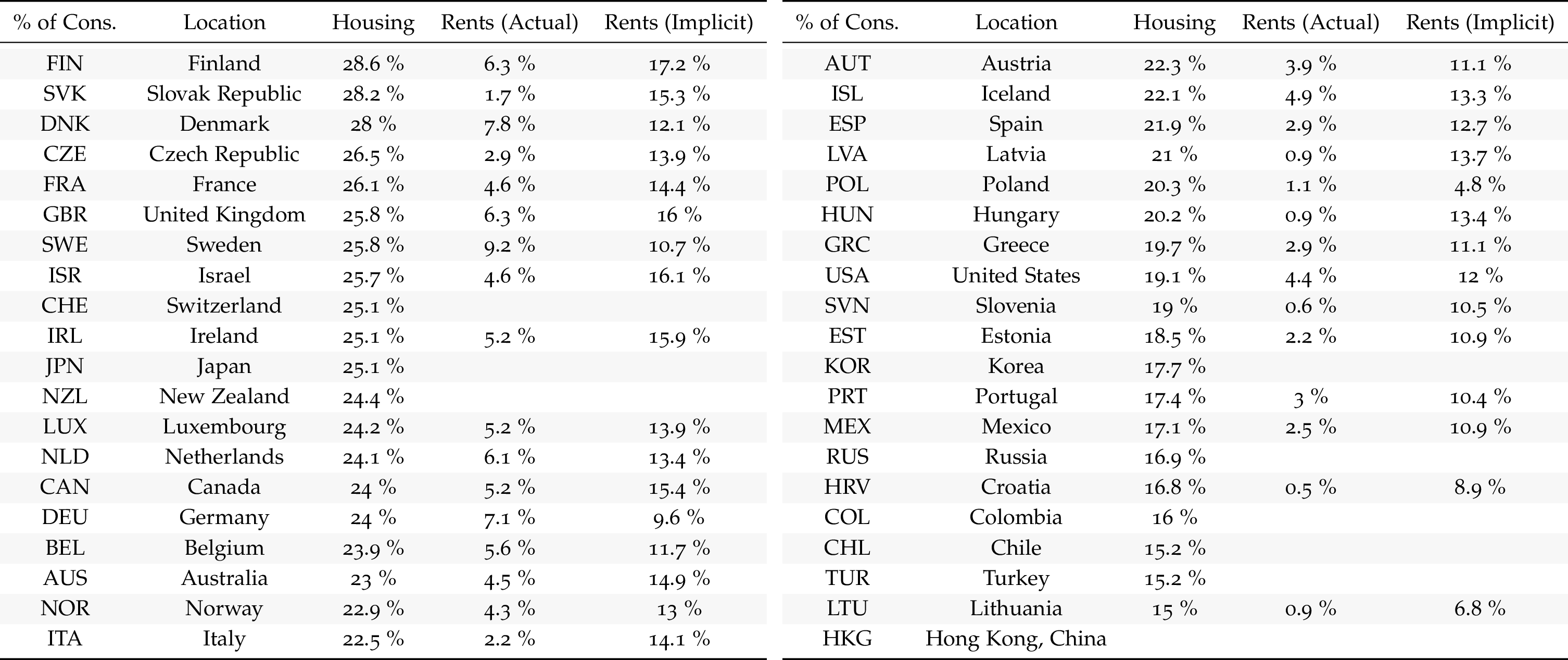
OECD - % of Consumption
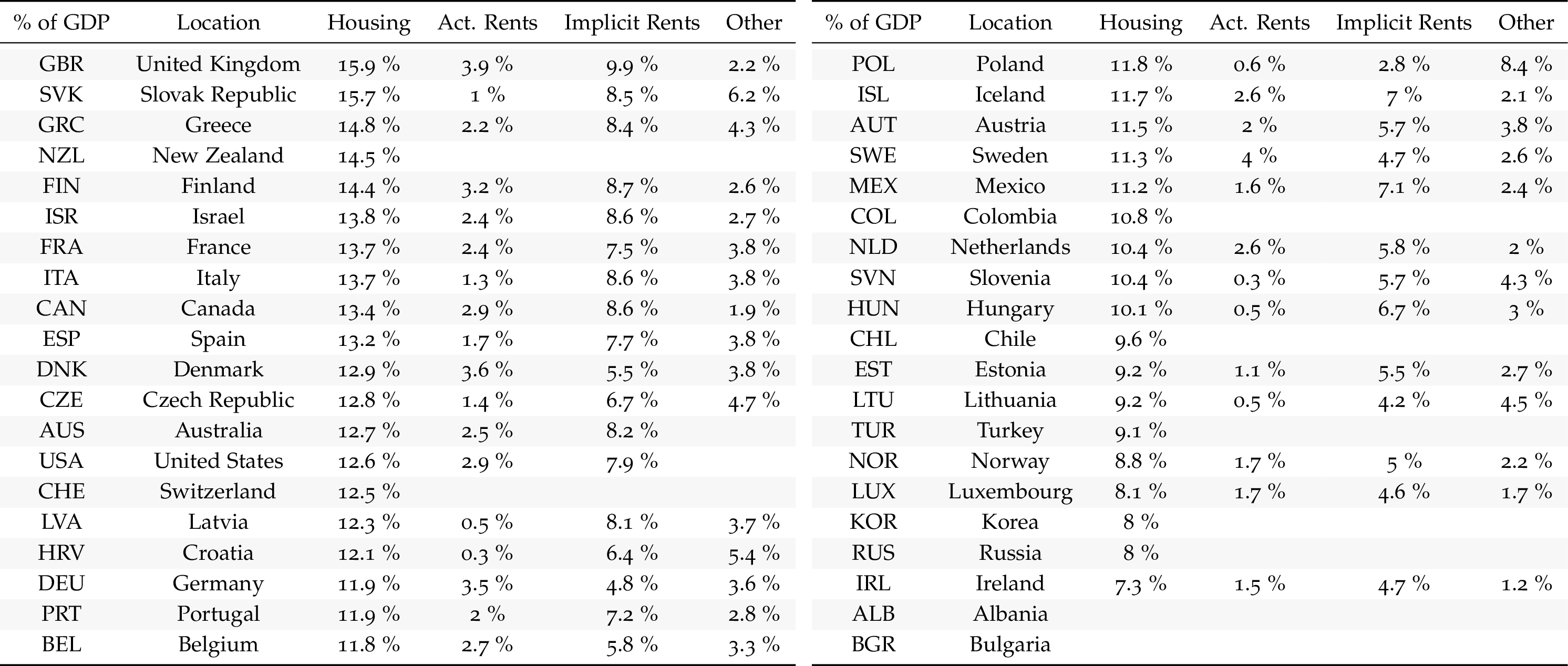
OECD - % of GDP
Consumption: Imputed VS Actual Rentals
Germany
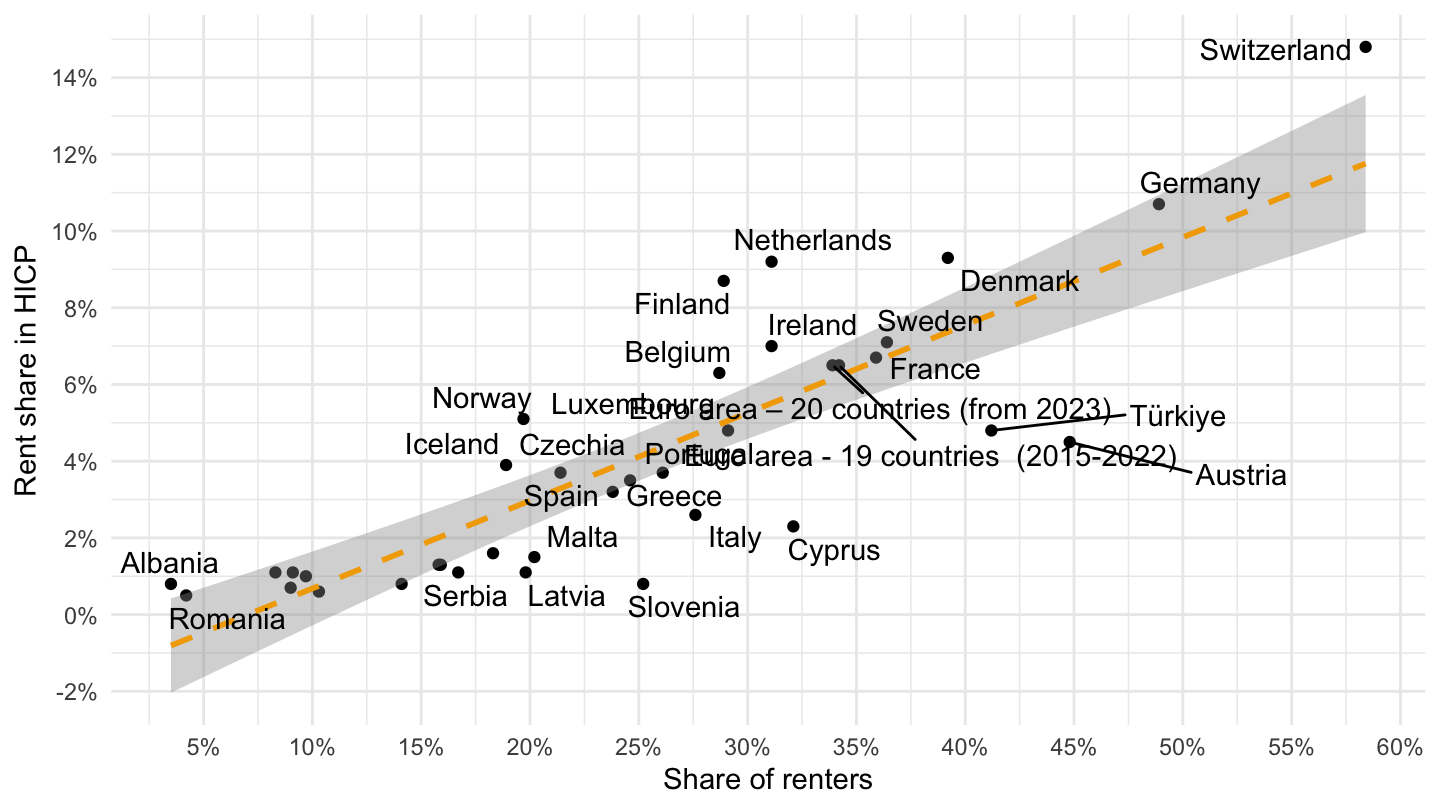
Tenure status 1/2

Tenure status 2/2

Importance of Housing in the Price Index
Housing in GDP

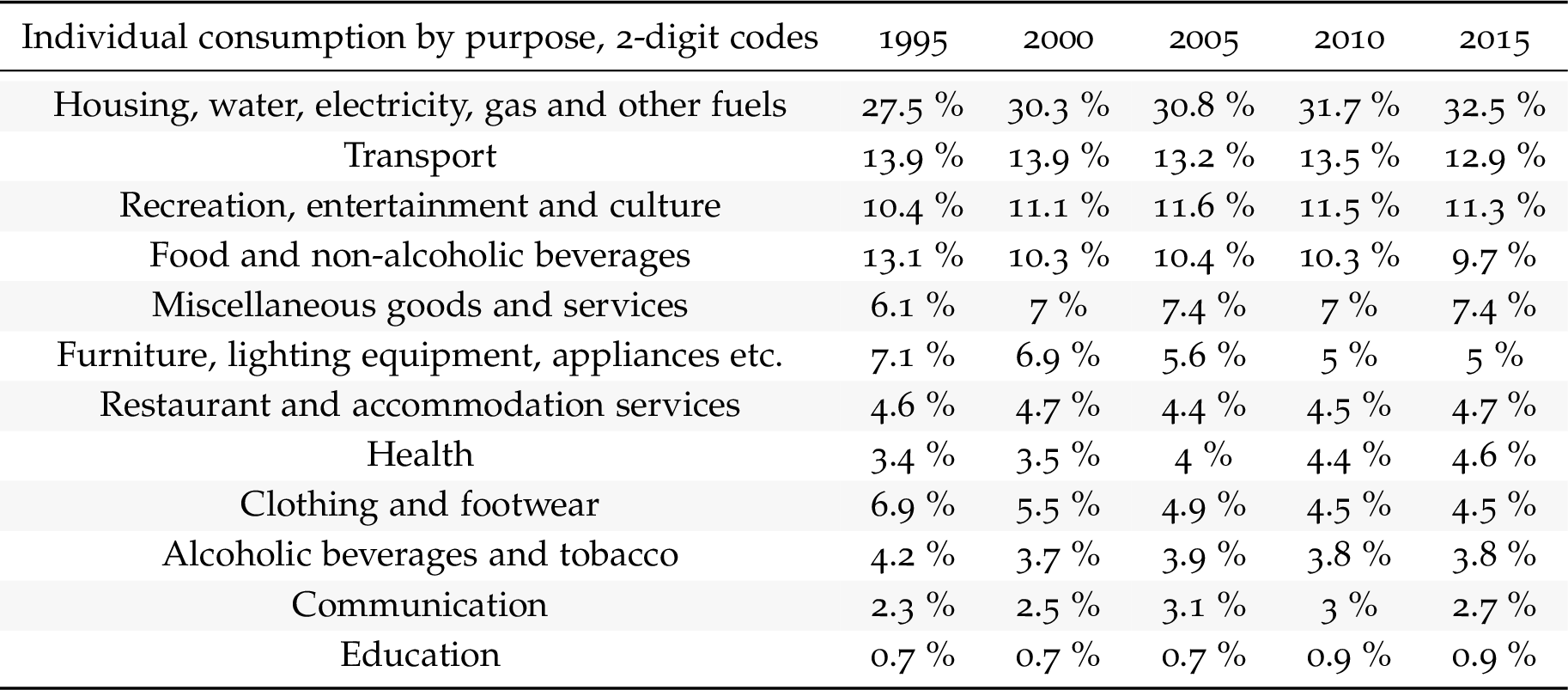
Weight of Housing in the CEX: Much bigger than this
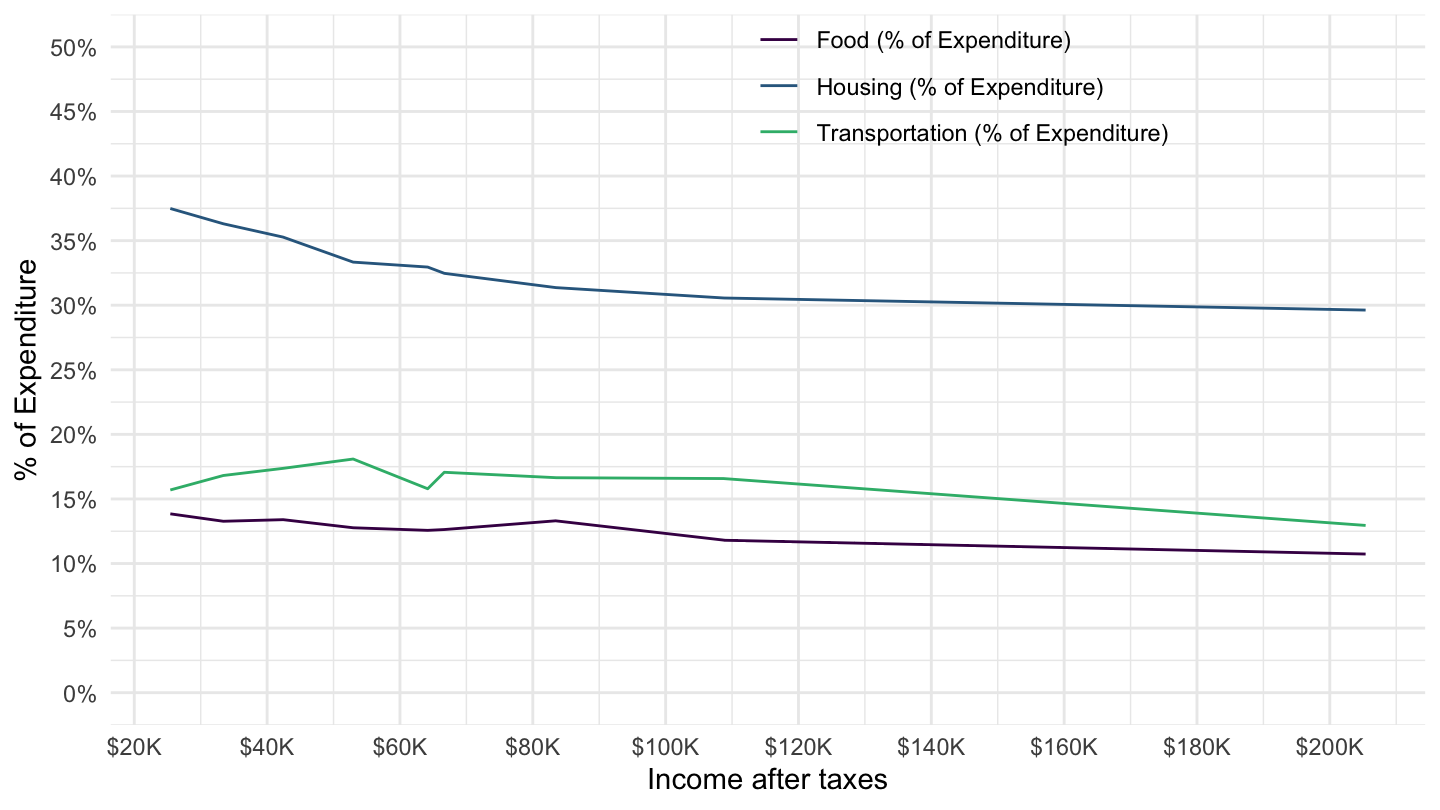
Weight of Housing in the CEX: Much bigger than this

How is housing measured in the
Data
Per Capita Mortgage Debt
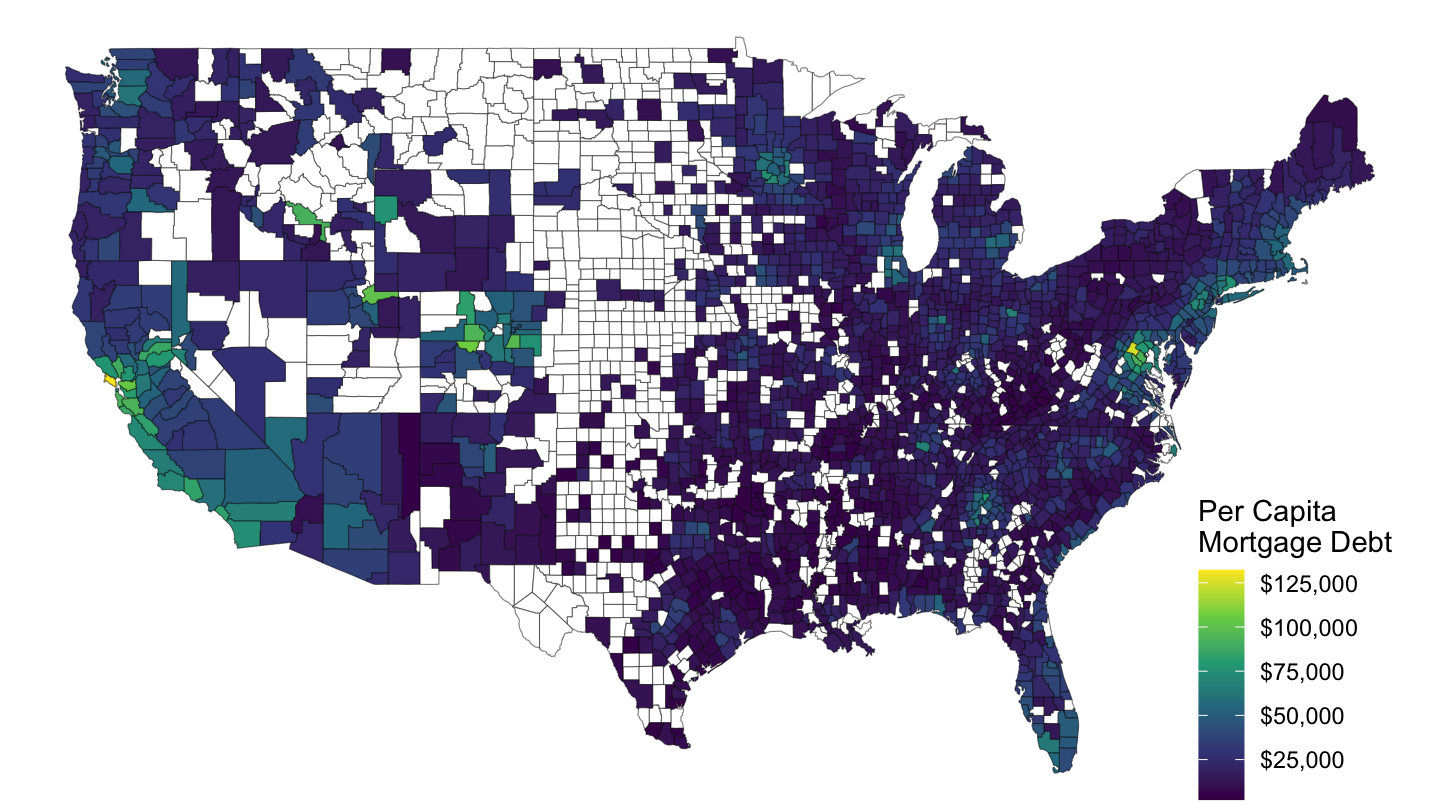
Per Capita Mortgage Debt

Land and dynamic inefficiency
Bernanke
Bernanke, thinking on the secular stagnation hypothesis:

The IMF Secular Stagnation Speech
Ben Bernanke’s criticism of secular stagnation
Responses to Bernanke
With a growing economy, the condition for dynamic inefficiency is \(r<g\). \(r\) need not be negative.
At that rate, it’s really not clear “it would pay to level the Rocky Mountains to save even the small amount of fuel expended by trains and cars that currently must climb steep grades”.
For that to be profitable, you would need the corresponding gain in fuel to be growing with \(g\), the rate of growth of the economy.
Idea
Discussion on land, and whether there exist enough long lived assets to store value.
In fact, to the extent that people want to own their homes, a fall in the interest rate may paradoxically lead to an increase in saving (note that the income effect would push in the same direction), which amplifies worries of secular stagnation.
Think of it really as “real-keynesian” economics. What about the very convincing evidence in Romer and Romer (2004) that monetary shocks have real effects. Once again, you should really think of shocks to the cost of housing as shocks to the nominal interest rate.
Kim and Lee (1997)
Title

Abstract

Problematic correction by Homburg (2014)
Presentation
Homburg (2014) argues that the argument in Kim and Lee (1997) is incorrect.
More generally: many (Most?) published papers are wrong. Including “corrections” to existing papers.
This one is a prime example. It pretends to have corrected Kim and Lee (1997) but in fact it is incorrect and misleading.
Lesson: you should read and think about papers critically !
Two Corrections
The paper makes two corrections. The first one is obvious, and does not contradict Kim and Lee (1997): it simply says that if taxation of rents is confiscatory (\(\tau=1\)) then taxing rents can lead to dynamic inefficiency. It is obvious, because from the market’s point of view, it is as if land was absent.
The second one, which is the one which is supposed to contradict Kim and Lee (1997), is actually incorrect. It is the last paragraph in the second part of the paper:
The property tax studied by Kim and Lee remains to be considered. This tax is imposed in period \(t+1\) on the land value in period \(t\) ; it diminishes the after-tax rent to \(\rho_{t+1}-\tau q_{t}\). If the property tax is non-confiscatory, the resulting equilibrium will be dynamically efficient, as argued in the preceding paragraph. However, if the property tax were confiscatory and eliminated the after-tax rent, land would become intrinsically worthless in the same manner as under a confiscatory tax on rent.
Cont’d
The previous paragraph that he refers to here is:
A tax on rent, as analyzed by Feldstein (1977), will also leave the arbitrage condition intact if and only if it is non-confiscatory. To see this one only has to replace the rent \(\rho_{t+1}\) by the after-tax rent \(\rho_{t+1} - \tau \rho_{t+1}\) in Eq. (1). Any tax rate below one hundred percent preserves the sign of the after-tax rent and validates the efficiency proof. Remembering that land opens a new market in the OLG model, a confiscatory tax on rent would close this market, making land as intrinsically worthless as Samuelson’s (1958) bubbly money. Inefficiency may then result.
where, for the sake of completeness, equation (1) is: \[\frac{q_{t+1}+\rho_{t+1}}{q_{t}}=1+r_{t+1}-\delta\]
Problem
Unfortunately, this argument made by Homburg (2014) is incorrect.
For while indeed replacing the rent \(\rho_{t+1}\) with \(\rho_{t+1} - \tau \rho_{t+1}\) does not change the value of the interest rate such that the value of land is finite. In the original case of equation (1): \[q = \frac{\rho}{r-\delta}\]
We find the well known result that the value of land is finite if the net interest rate is positive: \(r-\delta>0\).
Problem Cont’d
- Replacing the rent \(\rho_{t+1}\) with \(\rho_{t+1} - \tau \rho_{t+1}\) leads to: \[\frac{q_{t+1}+\rho_{t+1} - \tau \rho_{t+1}}{q_{t}}=1+r_{t+1}-\delta\] Therefore, the value of land at the steady state is: \[\boxed{q = \frac{\rho(1-\tau)}{r-\delta}}\] Again, this implies that the value of land is finite if the net interest rate is positive: \[\boxed{r-\delta>0}\]
Case of Property Tax
HOWEVER, if one instead replaces in equation (1) using a property tax (or a tax on transaction values, which is isomorphic to a property tax): \[\frac{q_{t+1}+\rho_{t+1} - \tau q_t}{q_{t}}=1+r_{t+1}-\delta\]
the value of land at the steady state is: \[\boxed{q = \frac{\rho}{r-\delta+\tau}}\]
This time, the net interest rate only needs to be higher than \(-\tau\) in order for the value of land to be finite, which implies that we may have dynamic inefficiency with a negative real interest rate: \[\boxed{r-\delta > -\tau}.\]
Bibliography
Homburg, Stefan. 2014. “Property Taxes and Dynamic Efficiency: A Correction.” Economics Letters 123 (3): 327–28. https://doi.org/10.1016/j.econlet.2014.03.013.
Kim, Kyung-Soo, and Jaewoo Lee. 1997. “Reexamination of Dynamic Efficiency with Taxation on Land.” Economics Letters 57 (2): 169–75. https://doi.org/10.1016/S0165-1765(97)00216-4.